Ile wychodzi z n=367?
Pytanie do zadania:
Jak dużą grupę osób należy zebrać, by szansa na to, że co najmniej dwie z nich mają urodziny tego samego dnia, była wyższa niż 50 proc.?
Chodzi o najmniejszą grupę dającą wynik powyżej 0.5.
Przy takim sformułowaniu, jakie cytujesz, nie chodzi o najmniejszą grupę, tylko o dowolną grupę, dla której prawdopodobieństwo wynosi więcej niż 0,5. Dla rozwiązania tego zadania trzeba rozwiązać nierówność:
>0,5)
Wśród 367 osób prawdopodobieństwo spotkania dwóch osób urodzonych tego samego dnia wynosi:
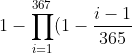=1)
Czyli 367 jest rozwiązaniem nierówności

Jeżeli chcemy najmniejszą grupę, to wtedy równanie:
\approx 0,5)
Z racji tego, co autor raczył był napisać, przyjrzeliśmy się wzorowi w kontekście bardziej ogólnym, stąd pytanie, co wyjdzie dla n>365.